Antoine Rolland, maître de conférence en statistique, chef  du département Statistique et informatique décisionnelle à l’Université Lyon 2, analyse avec une approche mathématique le pouvoir de chacun des groupes politiques au Parlement européen.

Les élections européennes du 26 mai 2019 sont l’occasion de se pencher sur la répartition du pouvoir au sein du Parlement européen. Le mode de scrutin de ces élections en fait un objet d’étude intéressant, les députés étant élus de manière croisée par pays et par affinité politique. Il en résulte un Parlement européen de 751 députés, que nous pouvons analyser suivant une grille de lecture nationale ou politique. Les modes de scrutins et les paysages politiques sont différents suivant les pays. La composition du Parlement européen reflète cette diversité en se structurant en 7 groupes plus les députés non-inscrits à un groupe.

Plusieurs articles ont déjà étudié le pouvoir réel de chaque pays au sein du Parlement européen, depuis 2001 et à l’occasion du (potentiel) Brexit¹²³; nous nous focaliserons uniquement dans cet article sur le pouvoir de chaque groupe politique.

Composition des groupes

En première analyse, on peut avoir une idée du pouvoir de chaque groupe en regardant le nombre de députés inscrits, comme indiqué dans le tableau 1.

Tableau 1 : répartition des groupes au Parlement européen par nombre de députés

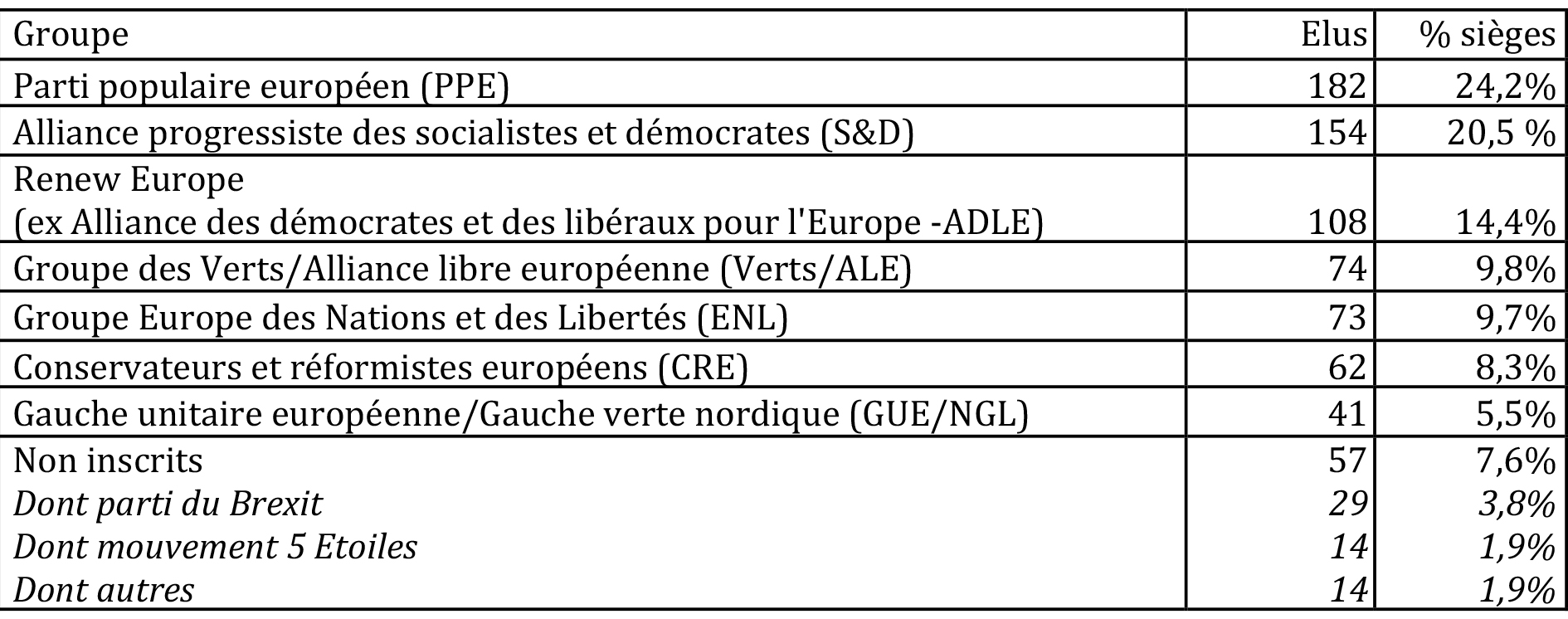
Comme abondamment commenté depuis l’élection, les deux groupes PPE et S&D continuent de peser le plus sur la vie du Parlement, sans toutefois disposer à eux deux de la majorité absolue. Ils sont cependant l’un et l’autre indispensables à la formation d’une coalition stable, compte tenu de l’isolement du groupe ENL, ainsi que d’au moins 43 des 57 députés non-inscrits (Parti du Brexit et Mouvement 5 étoiles).

Indice de pouvoir de Shapley-Shubik

Il est cependant connu que le nombre de députés composant un groupe ne donne qu’une vision imparfaite de la puissance de ce groupe au sein du Parlement, et ce tant pour des raisons politiques que pour des raisons mathématiques. D’un point de vue politique, l’influence d’un groupe parlementaire se fait sentir à travers sa capacité à trouver des compromis avec les autres groupes, à peser dans le travail de commission, à proposer les bonnes personnes pour les postes à responsabilité… Nous ne nous appesantirons pas sur cet aspect dans cet article. D’un point de vue mathématique, et en supposant un « vote bloqué par groupe », c’est-à-dire en supposant que tout un groupe vote de la même manière sur un sujet donné, alors le pouvoir d’un groupe dépend certes du nombre de ses députés, mais aussi du nombre de députés des autres groupes. Prenons l’exemple d’un Parlement fictif à trois groupes décrit dans l’exemple 1.

Exemple 1 : soit un Parlement à trois groupes A, B, C, de taille 49 députés pour le parti A, 49 députés pour le parti B, et 1 député pour le parti C. La majorité étant à 50 députés, il est évident que :

• Aucun groupe ne dispose de la majorité à lui tout seul
• Toute coalition de deux groupes quels qu’ils soient dispose de la majorité.

Il apparait donc que les trois groupes disposent du même pouvoir au sein de ce Parlement fictif, même si le rapport du nombre de députés est de 1 à 49.

Pour mesurer l’influence, ou le pouvoir réel d’un groupe au sein d’un Parlement, plusieurs auteurs ont proposé des « indices de pouvoir » pouvant se calculer mathématiquement. Nous nous intéresserons ici à l’indice de pouvoir de Shapley-Shubik⁴, entre autres indices existant (voir⁵ pour plus de détails) ; l’indice de Shapley-Shubik de groupe i, noté SS(i), est défini comme suit :

où i est le groupe dont on calcule l’indice SS(i), N l’ensemble de tous les groupes, S une coalition (un sous-ensemble) au sein de N, |S| le nombre de groupe de la coalition S et n le nombre de groupe total, et δ la fonction indicatrice valant 1 si S est une coalition gagnante (=majoritaire) et 0 sinon.

Exemple 1 (suite) : dans l’exemple 1, tous les groupes ont un indice SS de 1/3. Le détail des calculs est donné en annexe.

Il est alors possible, et facile, de calculer l’indice de Shapley-Shubik de chaque coalition. Comme il n’y a que 10 groupes (en séparant les non-inscrits en 3 sous-groupes) au Parlement européen, il n’y a « que » 3 628 800 permutations différentes à examiner, et l’indice se calcule rapidement avec un logiciel adapté. Le résultat est un indice compris entre 0 et 1 pour chaque groupe, la somme des indices étant égale à 1. Les résultats sont présentés dans le tableau 2, sous forme de pourcentage pour l’indice de pouvoir.

Analyse des indices de pouvoir de Shapley-Shubik par groupes

Tableau 2 : indices de pouvoir des groupes au parlement européen

Figure 1 : indices de pouvoir des groupes au parlement européen

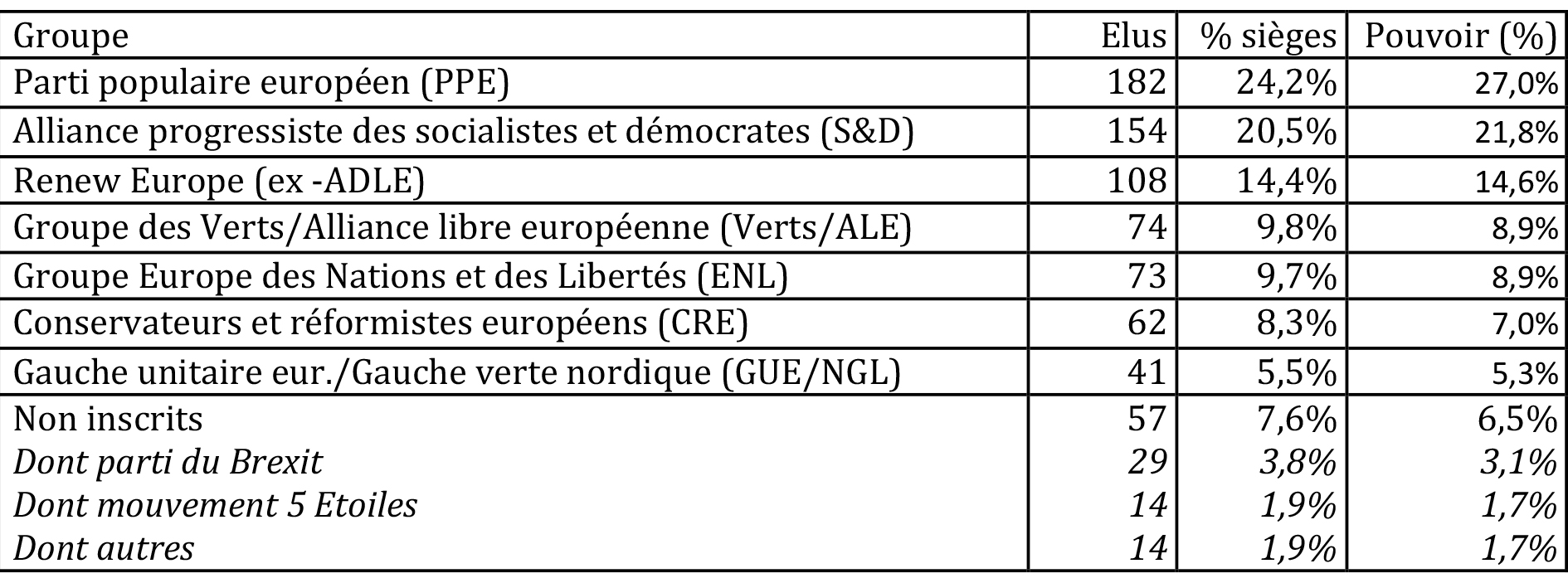
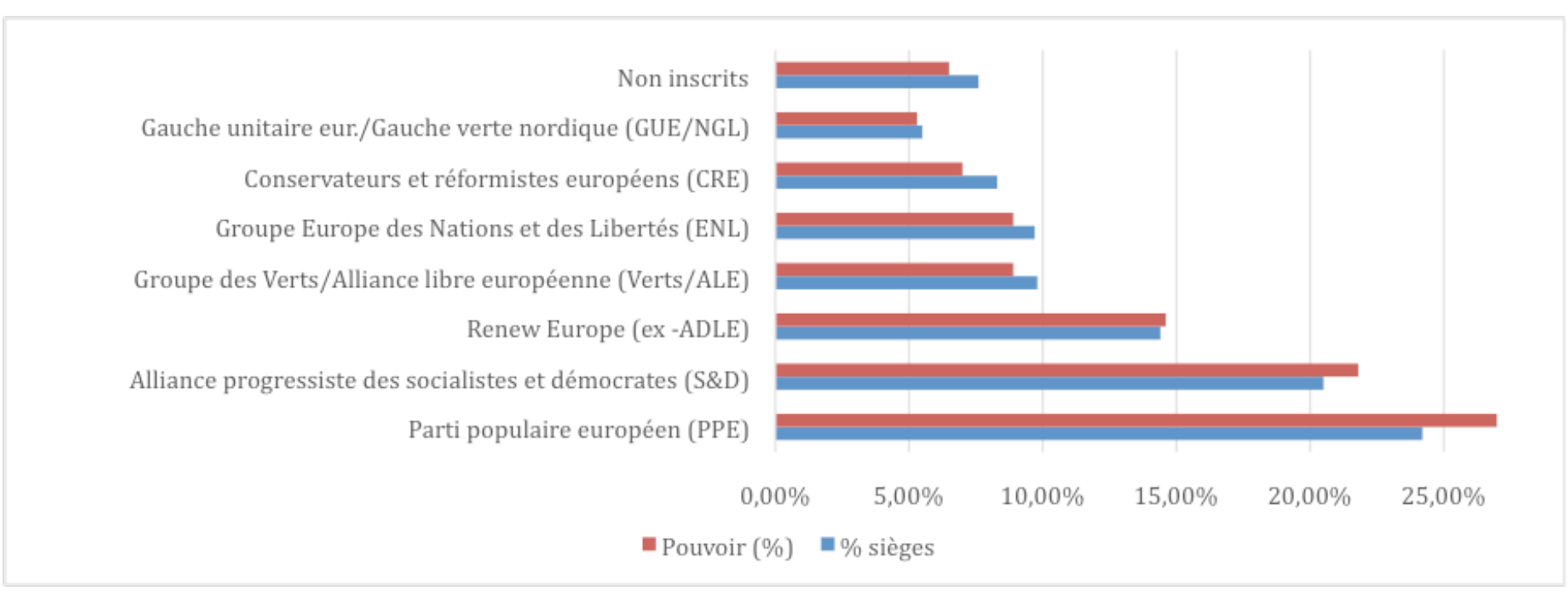
L’analyse des indices de Shapley-Shubik contenus dans le tableau 2, et présentés graphiquement dans la figure 1 met en évidence une « prime majoritaire ». En effet, les trois groupes dont l’indice de pouvoir est plus élevé que leur proportion de sièges au sein du Parlement sont le PPE (+2,8 points), les S&D (+1,3 point) et dans une moindre mesure Renew Europe (+0,2 point), c’est-à-dire les trois groupes les plus importants. Les groupes dont l’indice de pouvoir est moins élevé que leur proportion de sièges sont au contraire les groupes moins nombreux, en particulier les CRE (-1,3 point), les Verts/ALE (-0,9 point) et l’ENL (-0,8 point). L’importance des grands groupes est donc renforcée par leur position incontournable comme « membres obligés » de coalitions majoritaires. Les plus petits groupes parlementaires ne sont donc pas en position d’arbitres, contrairement à ce que les Verts/ALE ou l’ENL espéraient. Une fois encore, cette analyse se focalise sur l’aspect mathématique des coalitions possibles, sans rentrer dans des considérations de politique-fiction déterminant les coalitions plausibles.

Analyse de l’évolution des indices de pouvoir 2014-2019

Tableau 3 : indices de pouvoir des groupes au parlement européen – évolution 2014-2019

Figure 2 : indices de pouvoir des groupes au parlement européen – évolution 2014-2019

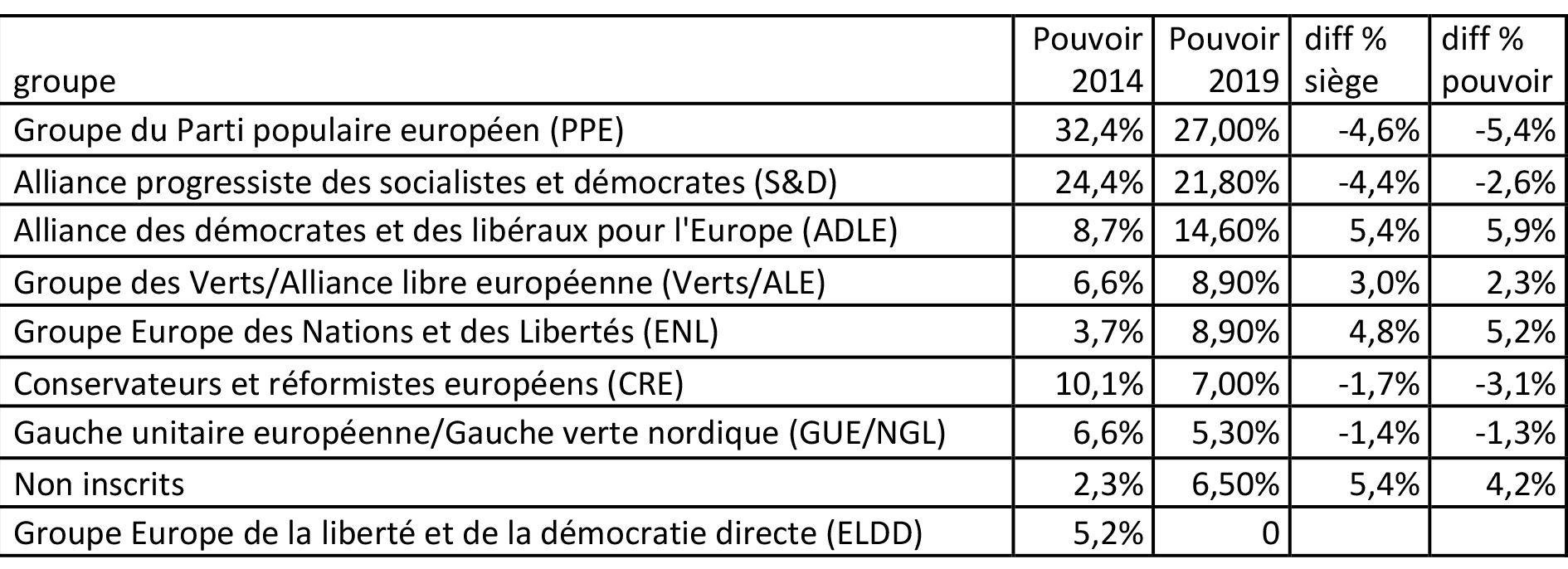
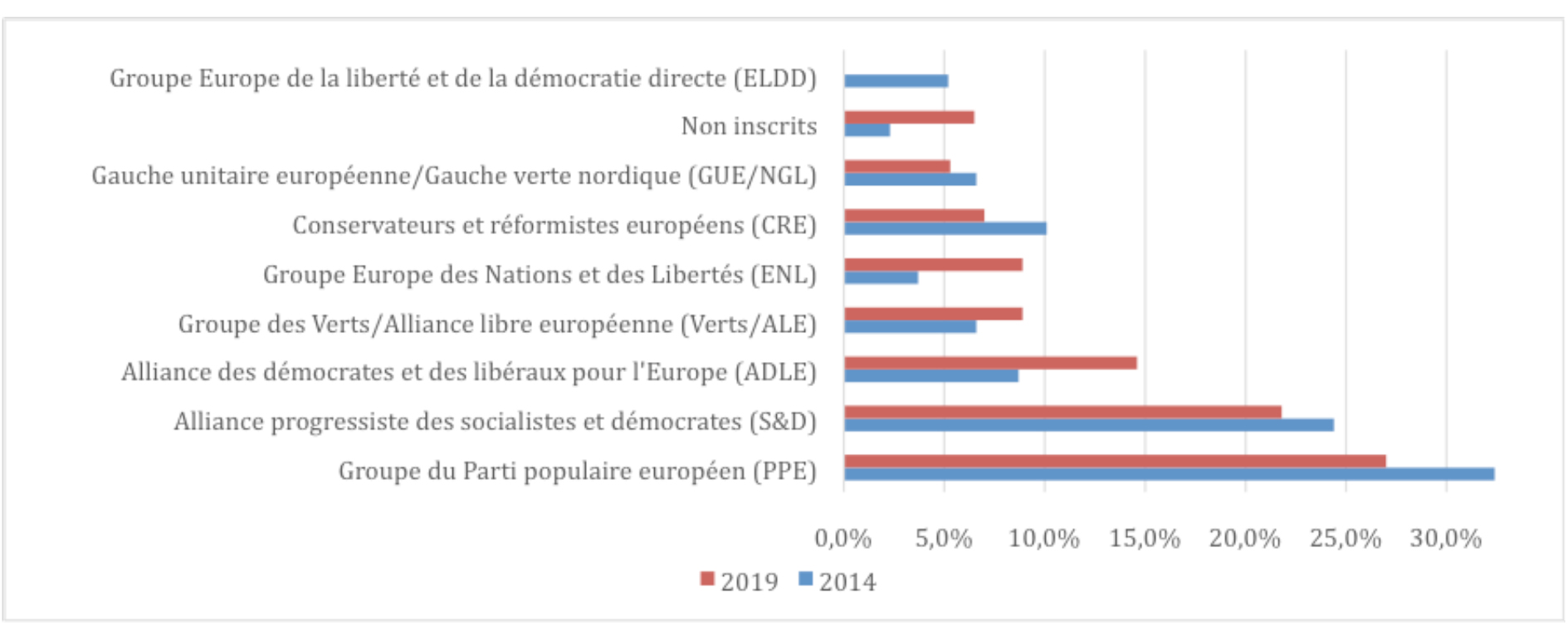
L’évolution des indices de pouvoir de chacun des groupes entre 2014 et 2019 est également instructive. Elle est présentée dans le tableau 3 et la figure 2. Cette évolution suit naturellement l’évolution du nombre de sièges de chaque groupe. La grande progression de ADLE/Renew Europe, du groupe ENL ainsi que, dans une moindre mesure, celle des Verts/ALE est particulièrement visible en terme d’indices de pouvoir. Le PPE et les CRE apparaissent comme les deux groupes perdant le plus de pouvoir au sein du parlement européen, tout en étant encore, pour le PPE, le groupe le plus influent. Même si l’équilibre général des groupes en présence change peu, on perçoit très nettement des différences de pouvoir au sein des grandes tendances : le PPE perd du pouvoir au profit de l’ADLE/Renew, le CRE perd du pouvoir au profit d’ENL, la GUE/NGL perd du pouvoir au profit des Verts/ALE.

°

°          °

Le calcul des indices de pouvoir de chaque groupe parlementaire ne révolutionne pas l’analyse des équilibres au sein du parlement européen. Il permet cependant de mettre en avant le rôle encore central du PPE malgré sa baisse d’influence entre 2014 et 2019 ; à l’inverse, il permet de pointer que la grande hausse du nombre de députés ENL ou Verts/ALE, que l’on voit également dans les indices de pouvoir, ne permet cependant pas à ces groupes de peser plus que leur poids réel, et même moins.

Antoine Rolland
Laboratoire ERIC, Université de Lyon